数据结构篇——二叉树的存储与遍历

     一、引入   

        书接上文，文于此续。上文我们学到了树的存储结构，那么今天，我们来学习下几种特殊的二叉树以及关于它的各种遍历，让我们一起加油吧。

二、特殊的二叉树

        二叉树的特殊形式这里介绍3种，其中需要着重记忆的有满二叉树和完全二叉树。其余1种大家了解认识即可。

1、斜树：

        就跟他的名字一样，所有结点只有左子树的叫做左斜树，只有右子树的叫做右斜树。具体图示如下：

2、满二叉树：

        满二叉树其实就是每个结点（除开叶子结点）的左右子树都齐全的树即深度为k且含有个结点的二叉树，如图所示：

        满二叉树的特点主要是：每一层上的结点树都是最大结点树，即每一层i的结点树都有最大值。 可以对满二叉树按层序编号:约定编号从根结点(根结点编号为1)起，自上而下，自左向右。由此就能引出完全二叉树的定义。

3、完全二叉树：

        深度为k、有n 个结点的二叉树，当且仅当其每个结点都与深度为k的满二叉树中编号为1~n的结点一一对应时，称为完全二叉树，如下图所示：

        完全二叉树的特点是：

这里提出两个关于完全二叉树的性质：

具有n个结点的完全二叉树的深度为不大于的最大整数。

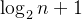如果对一颗有n个结点的完全二叉树（其深度为不大于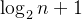的最大整数）的结点按层序编号，则对任意结点i有：      (1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲PARENT (i)是结点[i/2]。      (2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子LCHILD(t)是结点2i。      (3)如果2i+1>n,则结点i无右孩子;否则其右孩子RCHILD(i)是结点2i+1。

三、二叉树的存储结构 

        二叉树的存储结构和线性表类似，主要采用顺序和链式两种存储结构。

 1、顺序存储结构：

        顺序结构通常是采用一组连续的地址来存储数据，术语为了能够顺利的存储二叉树中的数据，就必须按照一定的规律来顺序来排放。

        对于完全二叉树来说，只要从根起按层序存储即可，依次从上至下，从左往右来存储树中的结点并编号。这样，编号为i的结点元素就会存储在一维数组中下标为i-1的分量当中。

        而对于一般二叉树来说，也按照完全二叉树那般排列，只是在一般二叉树中没有的部分就用“0”来表示，具体的图示如下：        从图中我们不难发现，这种顺序存储的结构只适用于完全二叉树，对于一般的二叉树来说就会造成大量的空间浪费。所以对于一般的二叉树来说更适合链式存储法。

2、链式存储法：

        同线性表的链式存储一般，想要实现一个链表就得确定其每一个结点的结构。对于二叉树来说，如下图所示的（a）它的结构主要分为数据域（data）、两个指向左右子树的指针域和一个指向双亲的指针域。通过这样分析我们就能确定其结构。那让我们仔细想想，指向双亲的指针域好像不是必要的。所以，我们就能发现，带有双亲指针域的存储结构多为三叉链表、反之则为二叉链表分别如下图中的（c）、（b）所示：

        关于二叉树的链式存储结构，可以参考下图理解：

         结合树的存储结构我们就能用代码表示出如下结构：

typedef struct BiTNode{
TElemType data; //结点数据域
struct BiTNode *lchild,*rchild; //左右子树指针域
}BiTNode,*BiTree;

四、二叉树的遍历 

        遍历二叉树是指从根结点开始，按照某条搜索路径了解寻访树中的每一个结点，使得树中的每一个结点都被访问一次且只被访问一次。其中主要的方法有先序遍历、中序遍历、后序遍历及其各种演化。

1、先序遍历：

        顾名思义，用自然语言表达则是：先访问根节点A，再按此规则递归遍历左子树（B – D – G – H），最后递归遍历右子树（C – E – I – F ），序列为A B D G H C E I F 。具体实现如下图所示：

具体的算法步骤如下：

代码描述：

void PreOrder(BiTree T){
if(T != NULL){
visit(T);//访问根节点
PreOrder(T->lchild);//递归遍历左子树
PreOrder(T->rchild);//递归遍历右子树
}
}

2、中序遍历：

        自然语言描述：先左子树（G – D – H ），再根节点（A ），后右子树（I – E – C – F ），序列为G D H B A I E C F 。具体实现如下图所示：

算法步骤：

代码描述：

void InOrder(BiTree T){
if(T != NULL){
InOrder(T->lchild);//递归遍历左子树
visit(T);//访问根结点
InOrder(T->rchild);//递归遍历右子树
}
}

 3、后序遍历：

        自然语言描述：先左子树（G – H – D ），再右子树（I – F – E ），最后根节点A，序列为G H D B I F E C A 。具体实现如下图所示：

算法步骤：

代码描述：

void PostOrder(BiTree T){
if(T != NULL){
PostOrder(T->lchild);//递归遍历左子树
PostOrder(T->rchild);//递归遍历右子树
visit(T);//访问根结点
}
}

 以上就是二叉树最基础的三种遍历方法了。先偷偷懒，咱下期再见。