深度学习 视觉处理(CNN) day_01

1. CNN 概述

        视觉处理三大任务：图像分类、目标检测、图像分割

        上游：提取特征，CNN

        下游：分类、目标、分割等，具体的业务

        卷积神经网络是深度学习在计算机视觉领域的突破性成果。在计算机视觉领域, 往往我们输入的图像都很大，使用全连接网络的话，计算的代价较高。另外图像也很难保留原有的特征，导致图像处理的准确率不高。         卷积神经网络（Convolutional Neural Network，CNN）是一种专门用于处理具有网格状结构数据的深度学习模型。最初，CNN主要应用于计算机视觉任务，但它的成功启发了在其他领域应用，如自然语言处理等。         卷积神经网络（Convolutional Neural Network）是含有卷积层的神经网络. 卷积层的作用就是用来自动学习、提取图像的特征。         卷积神经网络主要有三部分构成：卷积层、池化层和全连接层构成，其中卷积层负责提取图像中的局部特征；池化层用来大幅降低运算量并特征增强；全连接层类似神经网络的部分，用来输出想要的结果。

1.1 使用场景

1.2 与传统网络的区别

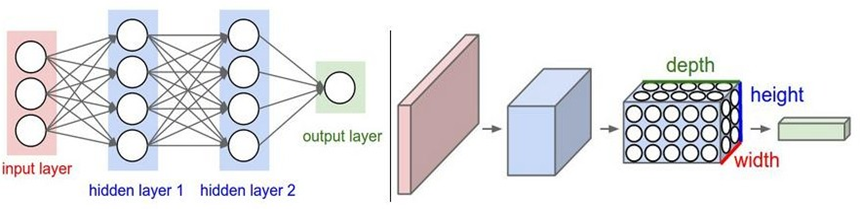
1.3 全连接的局限性

        全连接神经网络并不太适合处理图像数据。

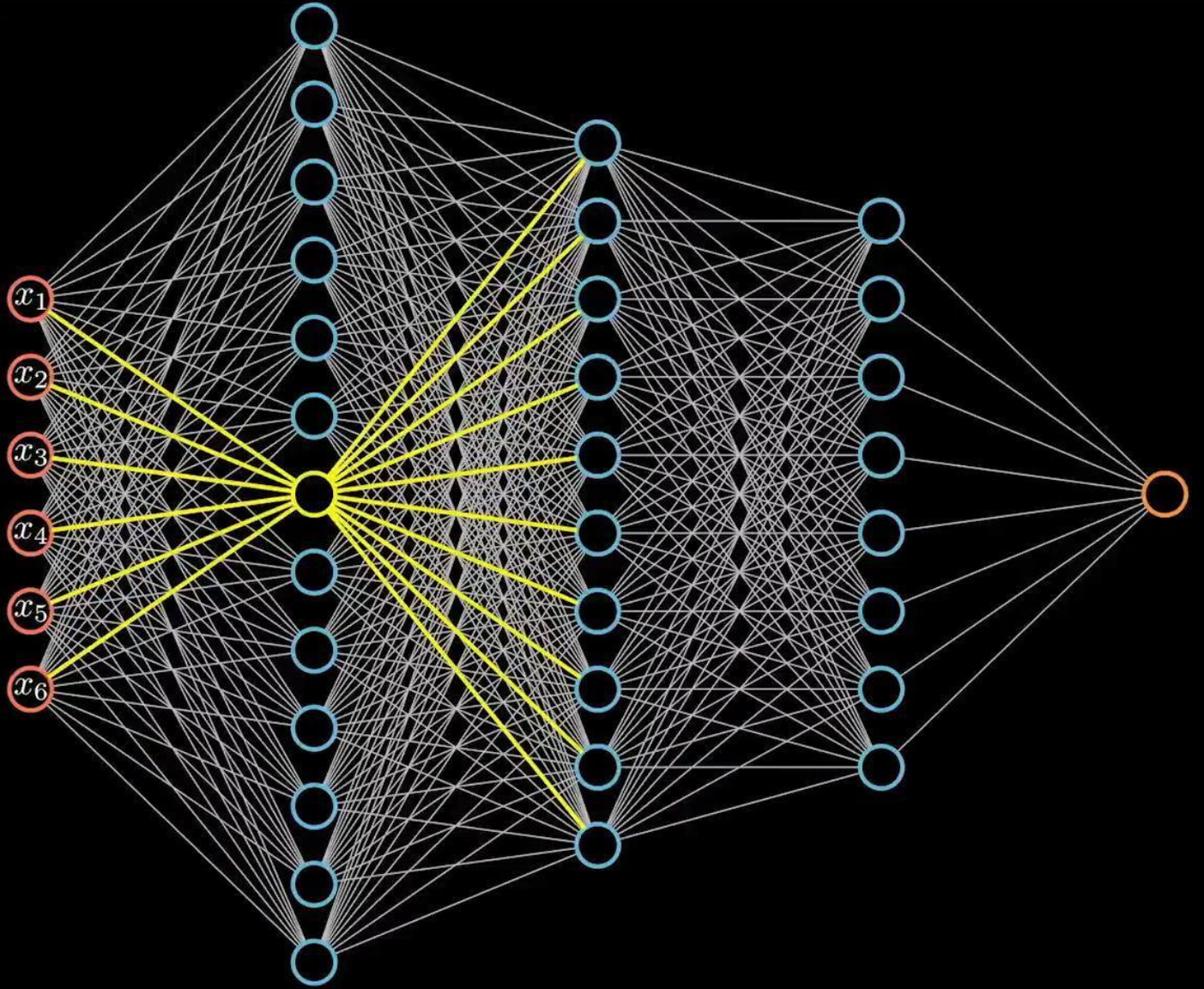
1.3.1 参数量巨大

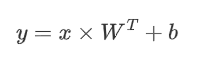
        全连接结构计算量非常大，假设我们有1000×1000的输入，如果隐藏层也是1000×1000大小的神经元，由于神经元和图像每一个像素连接，则参数量会达到惊人的1000×1000×1000×1000，仅仅一层网络就已经有个参数。

1.3.2 表达能力太有限

        全连接神经网络的角色只是一个分类器，如果将整个图片直接输入网络，不仅参数量大，也没有利用好图片中像素的空间特性，增加了学习难度，降低了学习效果。

1.4 卷积思想

        卷：从左往右，从上往下；积：乘积，求和

1.4.1 概念

        Convolution，输入信息与卷积核(滤波器,Filter)的乘积。 

1.4.2 局部连接

        – 局部连接可以更好地利用图像中的结构信息，空间距离越相近的像素其相互影响越大。         – 根据局部特征完成目标的可辨识性。

1.4.3 权重共享

        – 图像从一个局部区域学习到的信息应用到其他区域。         – 减少参数，降低学习难度。

2. 卷积层

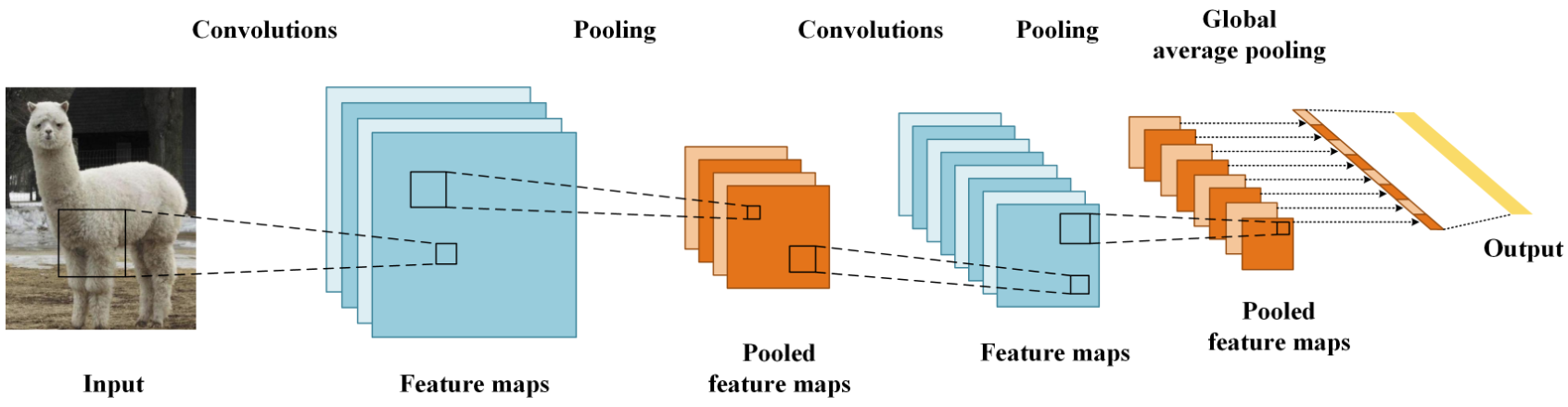
        接下来，我们开始学习卷积核的计算过程, 即: 卷积核是如何提取特征的。

2.1 卷积核

        卷积核是卷积运算过程中必不可少的一个“工具”，在卷积神经网络中，卷积核是非常重要的，它们被用来提取图像中的特征。         卷积核其实是一个小矩阵，在定义时需要考虑以下几方面的内容：                 – 卷积核的个数：卷积核（过滤器）的个数决定了其输出特征矩阵的通道数。                 – 卷积核的值：卷积核的值是初始化好的，后续进行更新。                 – 卷积核的大小：常见的卷积核有1×1、3×3、5×5等，一般都是奇数 × 奇数。

        下图就是一个3×3的卷积核：

2.2 卷积计算

2.2.1 卷积计算过程

        卷积的过程是将卷积核在图像上进行滑动计算，每次滑动到一个新的位置时，卷积核和图像进行点对点的计算，并将其求和得到一个新的值，然后将这个新的值加入到特征图中，最终得到一个新的特征图。

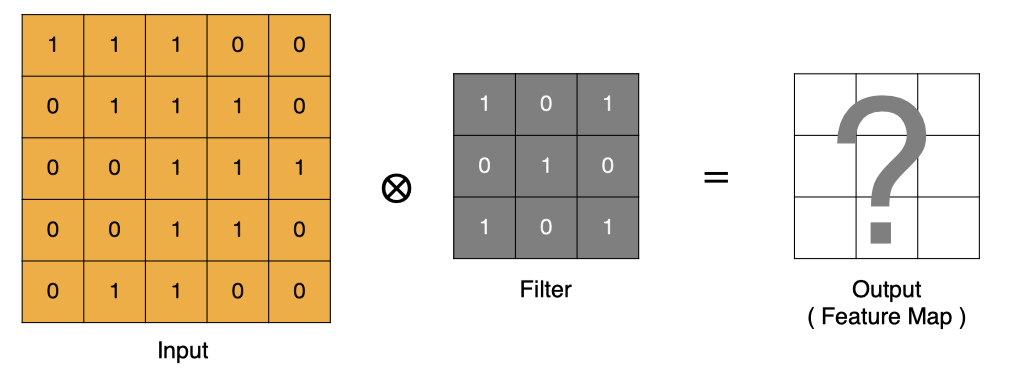
        1. input 表示输入的图像。         2. filter 表示卷积核, 也叫做滤波器。         3. input 经过 filter 的得到输出为最右侧的图像，该图叫做特征图。

​    那么, 它是如何进行计算的呢？卷积运算本质上就是在滤波器和输入数据的局部区域间做点积。

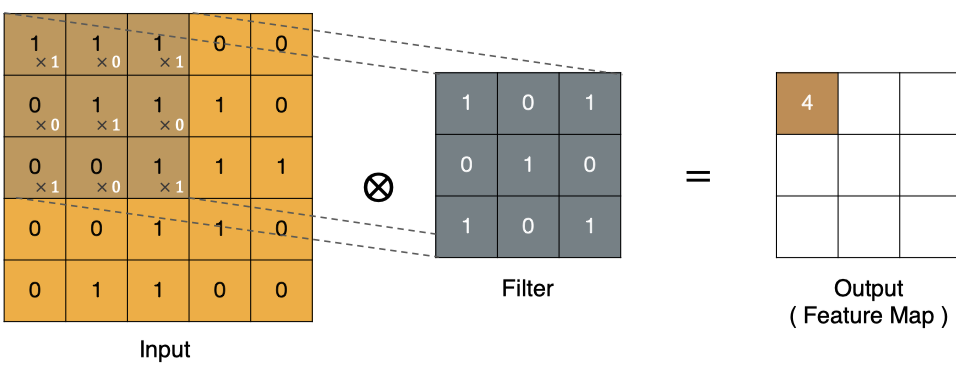
        左上角的点计算方法：

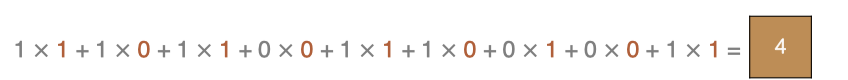
        按照上面的计算方法可以得到最终的特征图为:

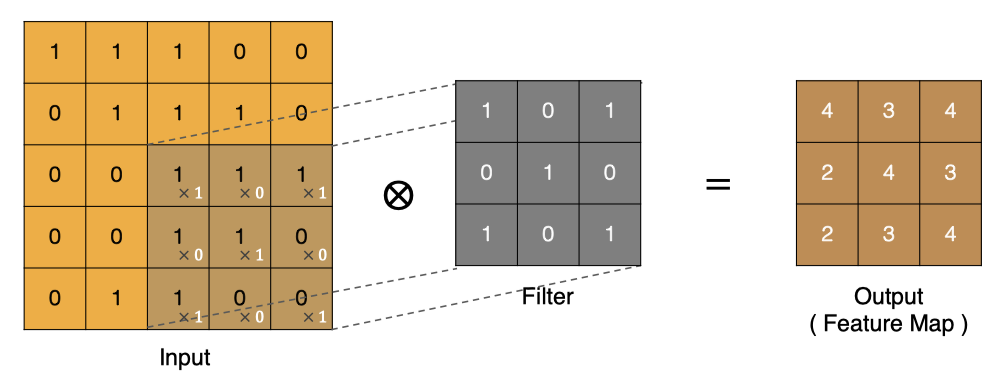
        卷积的重要性在于它可以将图像中的特征与卷积核进行卷积操作，从而提取出图像中的特征。         可以通过不断调整卷积核的大小、卷积核的值和卷积操作的步长，可以提取出不同尺度和位置的特征。         示例：

# 面向对象的模块化编程
from matplotlib import pyplot as plt
import os
import torch
import torch.nn as nn

def test001():
current_path = os.path.dirname(__file__)
img_path = os.path.join(current_path, "data", "彩色.png")
# 转换为相对路径
img_path = os.path.relpath(img_path)

# 使用plt读取图片
img = plt.imread(img_path)
print(img.shape)
# 转换为张量：HWC —> CHW —> NCHW 链式调用
img = torch.tensor(img).permute(2, 0, 1).unsqueeze(0)
# 创建卷积核 (501, 500, 4)
conv = nn.Conv2d(
in_channels=4, # 输入通道
out_channels=32, # 输出通道
kernel_size=(5, 3), # 卷积核大小
stride=1, # 步长
padding=0, # 填充
bias=True
)
# 使用卷积核对图像进行卷积操作 [9999] [[[[]]]]
out = conv(img)

# 输出128个特征图
conv2 = nn.Conv2d(
in_channels=32, # 输入通道
out_channels=128, # 输出通道
kernel_size=(5, 5), # 卷积核大小
stride=1, # 步长
padding=0, # 填充
bias=True
)
out = conv2(out)
print(out)
# 把图像显示出来
print(out.shape)
plt.imshow(out[0][10].detach().numpy(), cmap='gray')
plt.show()

# 作为主模块执行
if __name__ == "__main__":
test001()

2.2.2 卷积计算底层实现

        卷积计算底层实现并不是水平和垂直方向的循环。

        下图是卷积的基本运算方式：

        卷积真正的计算过程如下图：

2.3 边缘填充(Padding)

        通过上面的卷积计算，我们发现最终的特征图比原始图像要小，如果想要保持图像大小不变, 可在原图周围添加padding来实现。         更重要的，边缘填充还更好的保护了图像边缘数据的特征。

2.4 步长(Stride)

        按照步长为1来移动卷积核，计算特征图如下所示：

        如果我们把 Stride 增大为2，也是可以提取特征图的，如下图所示：

        注意：如果stride太小：重复计算较多，计算量大，训练效率降低；如果stride太大：会造成信息遗漏，无法有效提炼数据背后的特征。

2.5 多通道卷积计算

2.5.1 数字图像的标识

        我们知道图像在计算机眼中是一个矩阵。

        通道越多，可以表达的特征就越丰富。

2.5.2 具体计算实现

        实际中的图像都是多个通道组成的，我们怎么计算卷积呢

        计算方法如下：          1. 当输入有多个通道(Channel), 例如RGB三通道, 此时要求卷积核需要有相同的通道数。         2. 卷积核通道与对应的输入图像通道进行卷积。         3. 将每个通道的卷积结果按位相加得到最终的特征图。

        如下图所示：

2.6 多卷积核卷积计算

        实际对图像进行特征提取时, 我们需要使用多个卷积核进行特征提取。这个多个卷积核可以理解为从不同到的视角、不同的角度对图像特征进行提取。         那么, 当使用多个卷积核时, 应该怎么进行特征提取呢？

2.7 特征图大小

        输出特征图的大小与以下参数息息相关：

        那计算方法如下图所示：

        以下图为例：                 1. 图像大小: 5 x 5；                 2. 卷积核大小: 3 x 3；                 3. Stride: 1；                 4. Padding: 1；                 5. (5 – 3 + 2) / 1 + 1 = 5, 即得到的特征图大小为: 5 x 5

2.8 只卷一次

2.9 卷积参数共享

        数据是 32×32×3 的图像，用 10 个 5×5 的filter来进行卷积操作，所需的权重参数有多少个呢？

• 5×5×3 = 75，表示每个卷积核只需要75个参数。

• 10个不同的卷积核，就需要10*75 = 750个卷积核参数。

• 如果还考虑偏置参数b，最终需要 750+10=760 个参数。

2.10 局部特征提取

        通过卷积操作，CNN具有局部感知性，能够捕捉输入数据的局部特征，这在处理图像等具有空间结构的数据时非常有用。

2.11 PyTorch卷积层 API

        示例：test01 函数使用一个多通道卷积核进行特征提取, test02 函数使用 3 个多通道卷积核进行特征提取。

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import os

def showimg(img):
plt.imshow(img)
# 隐藏刻度
plt.axis("off")
plt.show()

def test001():
dir = os.path.dirname(__file__)
img = plt.imread(os.path.join(dir, "彩色.png"))
# 创建卷积核
# in_channels：输入数据的通道数
# out_channels：输出特征图数，和filter数一直
conv = nn.Conv2d(in_channels=4, out_channels=1, kernel_size=3, stride=1, padding=1)
# 注意：卷积层对输入的数据有形状要求 [batch, channel, height, width]
# 需要进行形状转换 H, W, C -> C, H, W
img = torch.tensor(img, dtype=torch.float).permute(2, 0, 1)
print(img.shape)
# 接着变形：CHW -> BCHW
newimg = img.unsqueeze(0)
print(newimg.shape)
# 送入卷积核运算一下
newimg = conv(newimg)
print(newimg.shape)

# 蒋NCHW->HWC
newimg = newimg.squeeze(0).permute(1, 2, 0)
showimg(newimg.detach().numpy())

# 多卷积核
def test002():
dir = os.path.dirname(__file__)
img = plt.imread(os.path.join(dir, "彩色.png"))
# 定义一个多特征图输出的卷积核
conv = nn.Conv2d(in_channels=4, out_channels=3, kernel_size=3, stride=1, padding=1)

# 图形要进行变形处理
img = torch.tensor(img).permute(2, 0, 1).unsqueeze(0)

# 使用卷积核对图片进行卷积计算
outimg = conv(img)
print(outimg.shape)
# 把图形形状转换回来以方便显示
outimg = outimg.squeeze(0).permute(1, 2, 0)
print(outimg.shape)
# showimg(outimg)
# 显示这些特征图
for idx in range(outimg.shape[2]):
showimg(outimg[:, :, idx].squeeze(-1).detach())

if __name__ == "__main__":
test002()

        效果：

2.12 卷积层实验

        原理：         在前面的章节中我们了解了卷积的过程，明白了卷积过程就是使用一个小的卷积核与输入特征矩阵进行滑动卷积的过程。         前面的章节中为了能更好的说清楚卷积的过程，其输入特征矩阵都是单通道的，根据“计算机眼中的图像”章节，知道单通道是灰度图或者二值化图，但是实际上识别图像大部分都是彩色图，也就意味着不是一个通道的特征输入。         所以，卷积的过程中大部分都是多通道的卷积，并且在卷积完之后还会加上偏置项。

        （1）特征输入

        在“特征输入”组件中，提供了一个3×3的三通道输入特征矩阵，并将其三个通道的内容都展示了出来。         也就意味着这个输入矩阵是一个3×3大小的，并且有三个通道。可以看成是三张3×3的A4纸“啪”一下，粘在一块了。

        （2）卷积核

        有了输入特征矩阵后，就需要定义卷积核了。         在“卷积核”组件中，为了简化计算，定义了卷积核的大小为2×2（实际上几乎不会有2×2的卷积核）， 通过拖动滑动条可以修改卷积核的个数。         并且为了能够对一个三通道的输入特征矩阵进行卷积，这里的每一个卷积核也是三通道的卷积核。

        （3）卷积过程显示

        在“卷积过程显示”组件中，固定了Padding方式为VALID和步长为1。

        在多通道卷积过程中，输出特征矩阵是由每个通道的卷积核与对应通道的输入特征矩阵在对应位置进行卷积，然后将多个通道的卷积结果相加的结果。         以输出特征矩阵的左上角“1”为例，其值是由第一个通道的卷积核与第一个通道的输入特征矩阵的左上角进行卷积加上第二个通道的卷积核与第二个通道的输入特征矩阵的左上角进行卷积加上第三个通道的卷积核与第三个通道的输入特征矩阵的左上角进行卷积，最后得到的卷积结果相加得到输出特征矩阵的左上角值为“1”，其他的以此类推。         在得到输出特征矩阵后，偏置矩阵就会与输出特征矩阵相加，得到本次多通道卷积的最终结果。         由此我们得到两个结论：

2.13 知识点扩展

3. 池化层

3.1 概述

        池化层 (Pooling) 降低空间维度, 缩减模型大小，提高计算速度. 即: 主要对卷积层学习到的特征图进行下采样（SubSampling）处理。         池化层主要有两种:         1. 最大池化（max  pooling）：最大池化是从每个局部区域中选择最大值作为池化后的值，这样可以保留局部区域中最显著的特征。最大池化在提取图像中的纹理、形状等方面具有很好的效果。         2. 平均池化（avgPooling）：平均池化是将局部区域中的值取平均作为池化后的值，这样可以得到整体特征的平均值。平均池化在提取图像中的整体特征、减少噪声等方面具有较好的效果。

3.2 池化层计算

        整体结构：

        计算：

        最大池化:

        平均池化:

3.3 步长(Stride)

        最大池化:

        平均池化:

3.4 边缘填充(Padding)

        最大池化:

        平均池化:

3.5 多通道池化计算

        在处理多通道输入数据时，池化层对每个输入通道分别池化，而不是像卷积层那样将各个通道的输入相加。这意味着池化层的输出和输入的通道数是相等。

3.6 池化层的作用

        池化操作的优势有：         1. 通过降低特征图的尺寸，池化层能够减少计算量，从而提升模型的运行效率。         2. 池化操作可以带来特征的平移、旋转等不变性，这有助于提高模型对输入数据的鲁棒性。         3. 池化层通常是非线性操作，例如最大值池化，这样可以增强网络的表达能力，进一步提升模型的性能。

        池化的缺点：池化操作会丢失一些信息，这是它最大的缺点；

3.7 池化API使用

        示例：

import torch
import torch.nn as nn

# 1. API 基本使用
def test01():

inputs = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]).float()
inputs = inputs.unsqueeze(0).unsqueeze(0)

# 1. 最大池化
# 输入形状: (N, C, H, W)
polling = nn.MaxPool2d(kernel_size=2, stride=1, padding=0)
output = polling(inputs)
print(output)

# 2. 平均池化
polling = nn.AvgPool2d(kernel_size=2, stride=1, padding=0)
output = polling(inputs)
print(output)

# 2. stride 步长
def test02():

inputs = torch.tensor([[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11], [12, 13, 14, 15]]).float()
inputs = inputs.unsqueeze(0).unsqueeze(0)

# 1. 最大池化
polling = nn.MaxPool2d(kernel_size=2, stride=2, padding=0)
output = polling(inputs)
print(output)

# 2. 平均池化
polling = nn.AvgPool2d(kernel_size=2, stride=2, padding=0)
output = polling(inputs)
print(output)

# 3. padding 填充
def test03():

inputs = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]).float()
inputs = inputs.unsqueeze(0).unsqueeze(0)

# 1. 最大池化
polling = nn.MaxPool2d(kernel_size=2, stride=1, padding=1)
output = polling(inputs)
print(output)

# 2. 平均池化
polling = nn.AvgPool2d(kernel_size=2, stride=1, padding=1)
output = polling(inputs)
print(output)

# 4. 多通道池化
def test04():

inputs = torch.tensor([[[0, 1, 2], [3, 4, 5], [6, 7, 8]],
[[10, 20, 30], [40, 50, 60], [70, 80, 90]],
[[11, 22, 33], [44, 55, 66], [77, 88, 99]]]).float()

inputs = inputs.unsqueeze(0)

# 最大池化
polling = nn.MaxPool2d(kernel_size=2, stride=1, padding=0)
output = polling(inputs)
print(output)

if __name__ == '__main__':
test04()

3.8 知识点扩展

4. 整体结构

4.1 特征图变化